
Matematicas
ANALISIS DE LA SEGUNDA DERIVADA
El análisis de segunda derivada se aplica principalmente en el estudio de funciones para determinar la concavidad y los puntos de inflexión, así como para identificar máximos y mínimos locales. Aquí hay algunos usos específicos:
Concavidad: La segunda derivada indica si la función es cóncava hacia arriba (si la segunda derivada es positiva) o cóncava hacia abajo (si es negativa).
Puntos de inflexión: Un punto de inflexión ocurre donde la segunda derivada cambia de signo, lo que indica un cambio en la concavidad de la función.
Máximos y mínimos locales: Si se encuentra un punto crítico (donde la primera derivada es cero), la segunda derivada se utiliza para determinar la naturaleza de ese punto:
- Si la segunda derivada es positiva en el punto crítico, hay un mínimo local.
- Si es negativa, hay un máximo local.
- Si es cero, el test es inconcluso y se necesita un análisis adicional.
La segunda derivada proporciona información crucial sobre el comportamiento y las propiedades de una función, lo que la hace una herramienta valiosa en análisis matemático y aplicaciones prácticas.
Ejercicios de ejemplo que muestren cuando una función es convexa o cóncava hacia arriba
Ejercicio 1:
Primero notemos que el dominio de la función es lnx/x
Ahora utilizaremos el criterio de concavidad-convexidad de la segunda derivada, el cual nos dice que la que función será convexa en los intervalos donde la segunda derivada sea positiva y será cóncava en los intervalos donde la segunda derivada sea negativa.
Primero procedemos a obtener la segunda derivada que es 2lnx-3/x
Luego procedemos a obtener los puntos donde la segunda derivada se anula, lo cual nos dará los puntos de inflexión.
Finalmente, analizamos en que intervalos la segunda derivada es positiva o negativa
Es cóncava hacia arriba en el intervalo (e3/2infinito) , es un resultado positivo por lo cual es cóncava hacia arriba ya que el resultado es positivo y el intervalo.
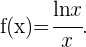
Ejercicios de ejemplo que muestren cuando una función es cóncava, o cóncava hacia abajo
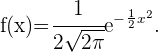
Ejercicio 1:
Primero notemos que el dominio de la función es la que se muestra en la imagen.
Ahora utilizaremos el criterio de concavidad-convexidad de la segunda derivada, el cual nos dice que la que función será convexa en los intervalos donde la segunda derivada sea positiva y será cóncava en los intervalos donde la segunda derivada sea negativa.
Primero procedemos a obtener la segunda derivada la cual se hace la respectivo procedminieto.
Luego procedemos a obtener los puntos donde la segunda derivada se anula, lo cualnos dará los puntos de inflexión
Finalmente, analizamos en que intervalos la segunda derivada es positiva o negativa
